
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo đầu bài thì hình vuông ABCD được ghép bởi 2 hình vuông nhỏ và 4 tam giác (trong đó có 2 tam giác to, 2 tam giác con). Ta thấy có thể ghép 4 tam giác con để được tam giác to đồng thời cũng ghép 4 tam giác con để được 1 hình vuông nhỏ. Vậy diện tích của hình vuông ABCD chính là diện tích của 2 + 2 x 4 + 2 x 4 = 18 (tam giác con). Do đó diện tích của hình vuông ABCD là:
18 x (10 x 10) / 2 = 900 (cm2)

\(S=3+\dfrac{3}{2}+\dfrac{3}{2^2}+...+\dfrac{3}{2^9}\\ 2S=6+3+\dfrac{3}{2}+...+\dfrac{3}{2^8}\\ 2S-S=\left(6+3+\dfrac{3}{2}+...+\dfrac{3}{2^8}\right)-\left(3+\dfrac{3}{2}+\dfrac{3}{2^2}+...+\dfrac{3}{2^9}\right)\\ S=6-\dfrac{3}{2^9}\\ S=6-\dfrac{3}{512}\\ S=5\dfrac{509}{512}\)


A = \(\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{110}+\dfrac{1}{132}\)
=> A = \(\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}+\dfrac{1}{10.11}+\dfrac{1}{11.12}\)
=> A = \(\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{11}-\dfrac{1}{12}\)
=> A = \(\dfrac{1}{5}-\dfrac{1}{12}\)
=> A = \(\dfrac{7}{60}\)
Vậy A = \(\dfrac{7}{60}\)
Ta có:
A = \(\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{110}+\dfrac{1}{132}\)
= \(\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}+\dfrac{1}{10.11}+\dfrac{1}{11.12}\)
= \(\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{12}\)
= \(\dfrac{1}{5}-\dfrac{1}{12}\) = \(\dfrac{7}{60}\)

Gọi d là ƯCLN(2n+5,n+3)(d\(\in\)N*)
Ta có:\(2n+5⋮d,n+3⋮d\)
\(\Rightarrow2n+5⋮d,2\cdot\left(n+3\right)⋮d\)
\(\Rightarrow2n+5⋮d,2n+6⋮d\)
\(\Rightarrow\left(2n+6\right)-\left(2n+5\right)⋮d\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
Vì ƯCLN(2n+5,n+3)=1
\(\Rightarrow\frac{2n+5}{n+3}\) là phân số tối giản
Gọi d là ƯCLN(2n+5,n+3)(d∈
N*)
Ta có:2n+5⋮d,n+3⋮d
⇒2n+5⋮d,2⋅(n+3)⋮d
⇒2n+5⋮d,2n+6⋮d
⇒(2n+6)−(2n+5)⋮d
⇒1⋮d⇒d=1
Vì ƯCLN(2n+5,n+3)=1

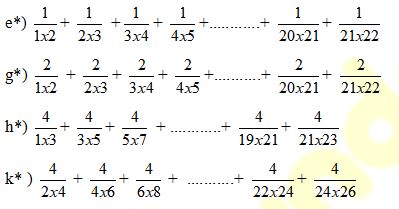


 có giá trị là số nguyên.
có giá trị là số nguyên.


