
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mình không thấy câu nào cả thì giúp kiểu gì lỗi ảnh hay sao ý

ĐKXĐ: \(x+2y\ne0\)
\(\left\{{}\begin{matrix}x-\dfrac{1}{x+2y}=\dfrac{7}{4}\\-\dfrac{5}{2}x+2+\dfrac{4}{x+2y}=-2\end{matrix}\right.\)
Đặt \(\dfrac{1}{x+2y}=z\) ta được hệ:
\(\left\{{}\begin{matrix}x-z=\dfrac{7}{4}\\-\dfrac{5}{2}x+4z=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\z=\dfrac{1}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{x+2y}=\dfrac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\x+2y=4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

b) \(\sqrt{x^2}=\left|-8\right|\)
\(\Rightarrow\left|x\right|=8\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)
d) \(\sqrt{9x^2}=\left|-12\right|\)
\(\Rightarrow\sqrt{\left(3x\right)^2}=12\)
\(\Rightarrow\left|3x\right|=12\)
\(\Rightarrow\left[{}\begin{matrix}3x=12\\3x=-12\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{12}{3}\\x=-\dfrac{12}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)

ĐKXĐ: \(\left\{{}\begin{matrix}2x-3>=0\\x+1>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\x>=-1\end{matrix}\right.\)
=>\(x>=\dfrac{3}{2}\)
\(\sqrt{2x-3}-\sqrt{x+1}=x-4\)
=>\(\dfrac{2x-3-x-1}{\sqrt{2x-3}+\sqrt{x+1}}-\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(\dfrac{1}{\sqrt{2x-3}+\sqrt{x+1}}-1\right)=0\)
=>x-4=0
=>x=4(nhận)

Gọi số xe dự định tham gia chở hàng là x (xe) với x>4, x nguyên dương
Mỗi xe dự định chở khối lượng hàng là: \(\dfrac{20}{x}\) (tấn)
Số xe thực tế tham gia chở hàng là: \(x-4\) (xe)
Thực tế mỗi xe phải chở số hàng là: \(\dfrac{20}{x-4}\) (tấn)
Do thực tế mỗi xe phải chở nhiều hơn dự định là 5/6 tấn hàng nên ta có pt:
\(\dfrac{20}{x-4}-\dfrac{20}{x}=\dfrac{5}{6}\)
\(\Rightarrow24x-24\left(x-4\right)=x\left(x-4\right)\)
\(\Leftrightarrow x^2-4x-96=0\)
\(\Rightarrow\left[{}\begin{matrix}x=12\\x=-8\left(loại\right)\end{matrix}\right.\)
Vậy thực tế có \(12-4=8\) xe tham gia vận chuyển

M A O B E F H K P Q
a/
Ta có
AE = HE; BF = HF (2 tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau)
=> AE + BF = HE + HF = EF (dpcm)
b/ Gọi P; K; Q lần lượt là giao của OE; OM; OF với (O)
Ta có
sđ cung PA = sđ cung PH (Hai tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn thì đường nối điểm đó với tâm chia đôi cung chắn bởi 2 tiếp điểm)
sđ cung QB = sđ cung QH (lý do như trên)
=> sđ cung PH + sđ cung QH = sđ cung PA + sđ cung QB
=> sđ cung APH = sđ cung BQH
Mà sđ cung APH + sđ cung BQH = sđ cung AKB
=> sđ cung APH = sđ cung BQH = \(\dfrac{sđcungAKB}{2}\) (1)
Ta có
sđ cung KA = sđ cung KB (Hai tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn thì đường nối điểm đó với tâm chia đôi cung chắn bởi 2 tiếp điểm)
Mà sđ cung KA + sđ cung KB = sđ cung AKB
=> sđ cung KA = sđ cung KB = \(\dfrac{sđcungAKB}{2}\) (2)
Ta có
\(sđ\widehat{MOA}=sđcungKA=\dfrac{sđcungAKB}{2}\) (góc ở tâm đường tròn) (3)
\(sđ\widehat{FOE}=sđcungPHQ=sđcungPH+sđcungQH=\dfrac{sđcungAKB}{2}\) (góc ở tâm đường tròn) (4)
Từ (1) (2) (3) (4) \(\Rightarrow\widehat{MOA}=\widehat{FOE}\)

\(x^2+3x+2+2\left(2-x\right)\sqrt{x-1}=0\left(x\ge1\right)\)
\(\Leftrightarrow x^2-x-2x+2-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow x\left(x-1\right)-2\left(x-1\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-2\right)\sqrt{x-1}\left(\sqrt{x-1}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\\sqrt{x-1}=0\\\sqrt{x-1}-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x-1=0\\\sqrt{x-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=1\left(tm\right)\\x-1=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=5\end{matrix}\right.\left(tm\right)\)
Vậy: \(x\in\left\{1;2;5\right\}\)

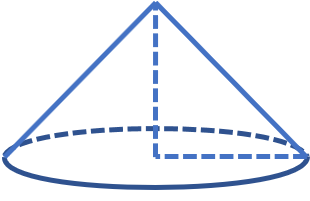
Thể tích của phần còn lại bằng thể tích của hình trụ tròn trừ đi thể tích của phần hình nón tiện.
V(hình trụ) = πr²h =π10²20= 2000π
V(nón) = 1/3 . πr²h(nón) =1/3 .π10². 10
V(cần tính) = V(hình trụ) - V(nón)
=2000π - 1000π/3
=5000π /3 (cm3)





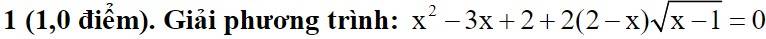
A B C H D E
a/ Ta có
H và E cùng nhìn AC dưới 1 góc vuông nên H và E thuộc đường tròng đường kính AC => AHEC là tứ giác nội tiếp đường tròn đường kính AC tâm I là trung điểm của AC
b/
Xét tg vuông ABH và tg vuông ABC có
\(\widehat{BAH}=\widehat{ACH}\) (cùng phụ với \(\widehat{ABC}\) ) (1)
Xét tg vuông ABH và tg vuông ADH có
AH chung
BH=DH (gt)
=> tg ABH = tg ADH (Hai tg vuông có hai cạnh góc vuông bằng nhau) \(\Rightarrow\widehat{BAH}=\widehat{DAH}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{DAH}=\widehat{ACH}\)
Xét tứ giác nội tiếp AHEC có
\(\widehat{ACH}=\widehat{AEH}\) (góc nội tiếp cùng chắn cung AH) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{AEH}=\widehat{DAH}\) => tg AHE cân tại H (td có hai góc ở đáy bằng nhau)
c/
Ta có
\(\widehat{DAH}=\widehat{ACH}\) (cmt)
Xét tứ giác nội tiếp AHEC có
\(\widehat{DAH}=\widehat{ECH}\) (góc nội tiếp cùng chắn cung HE)
\(\Rightarrow\widehat{ACH}=\widehat{ECH}\) => CB là tia phân giác của \(\widehat{ACE}\)