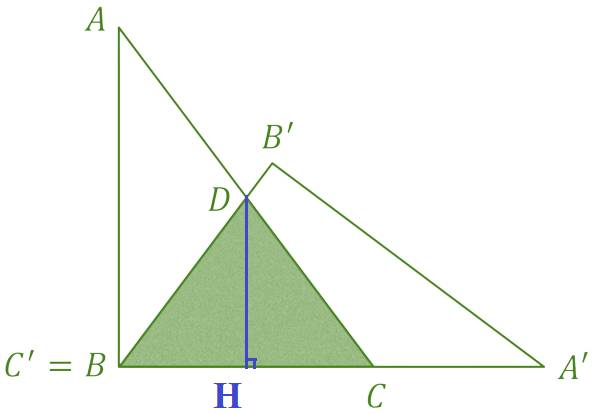
Kẻ đường cao DH của tam giác BDC
Ta có : \(\Delta ABC=\Delta A'B'C'\)
=> \(\widehat{DBC}=\widehat{DCB}\) (1)
=> \(\widehat{DAB}=\widehat{DBA}\) (2) (cùng phụ 2 góc (1))
Từ (1) (2) => AD = BD = DC = \(\dfrac{1}{2}AC\) => D trung điểm AC
mà DH//BA nên DH đường trung bình tam giác ABC
=> \(DH=\dfrac{1}{2}AB\)
Lại có \(P=\dfrac{S_{CBD}}{S_{BADB'A'}}=\dfrac{\dfrac{DH.BC}{2}}{S_{ABC}+S_{A'B'C'}-S_{CBD}}=\dfrac{\dfrac{DH.BC}{2}}{2S_{ABC}-S_{CBD}}\)
\(=\dfrac{\dfrac{DH.BC}{2}}{AB.BC-\dfrac{DH.BC}{2}}=\dfrac{\dfrac{AB.BC}{4}}{AB.BC-\dfrac{AB.BC}{4}}=\dfrac{\dfrac{1}{4}}{1-\dfrac{1}{4}}=\dfrac{1}{3}\)









