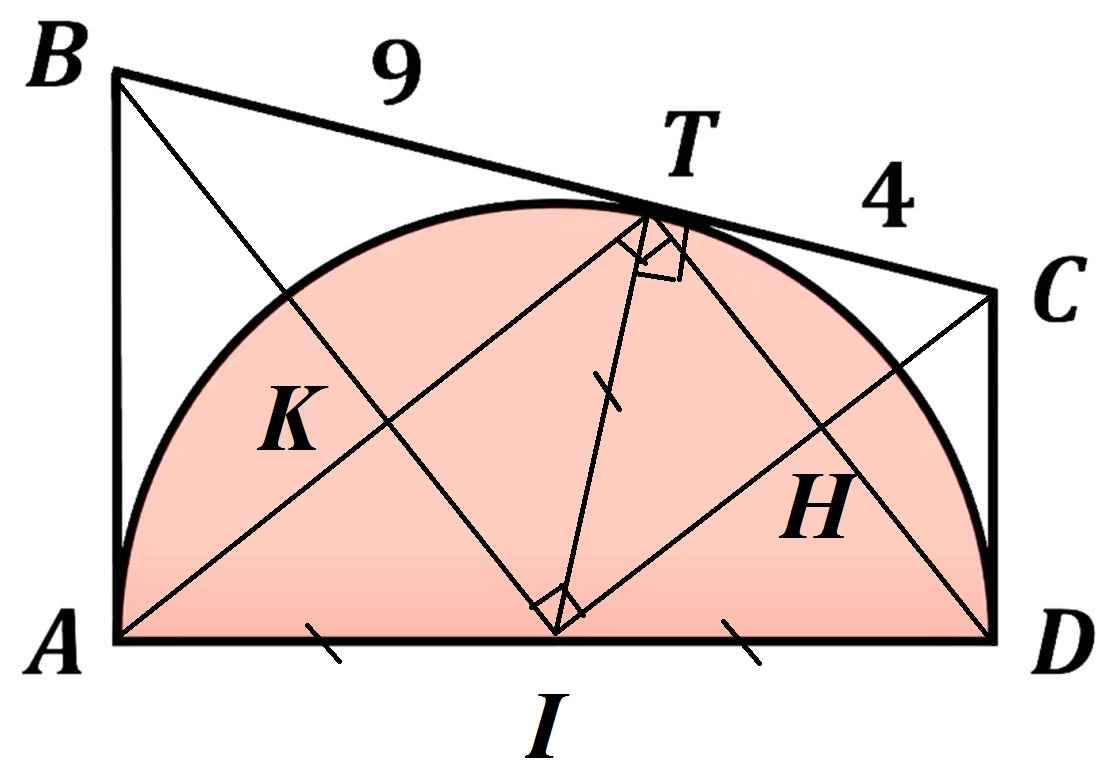
Xét nửa đường tròn (I,ID) có tam giác ATD nội tiếp (I)

=> Tam giác ATD vuông tại T => \(\widehat{ATD}=90^{\text{o}}\) (1)

Lại có BC , BA,CD là các tiếp tuyến của I với tiếp điểm lần lượt là T,A,D

=> \(\widehat{BAI}=\widehat{BTI}=\widehat{CDI}=90^{\text{o}}\)

Từ đó ta thấy \(\Delta BAI=\Delta BTI\) 

=> BT = BA và \(\widehat{ABI}=\widehat{TBI}\)

=> \(\Delta ABK=\Delta TBK\) 

=> \(BK\perp AT\) (2)

tương tự ta chứng minh được : \(CH\perp DT\) (3)

Từ (1);(2) ;(3) ta thấy \(\widehat{BIC}=90^{\text{o}}\) hay tam giác BIC vuông tại I 

lại có IT là đường cao

Áp dụng hệ thức lượng ta có \(IT^2=BT.TC=9.4=36\Leftrightarrow IT=6=r\) (đvđd)

Diện tích nửa đường tròn (I,IT) = \(S=\dfrac{1}{2}\pi.r^2=18\pi\) (đvdt)