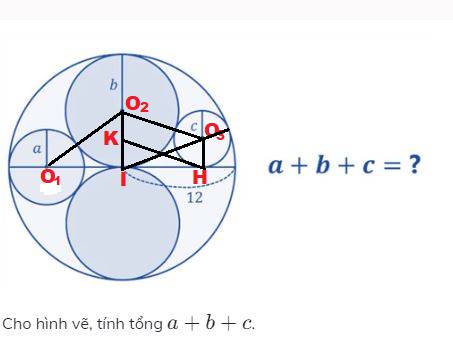
Kẻ \(O_2I\perp IH,O_3I\perp IH,HK//O_2O_3\)
Ta có: 2b = 12 => b = 6
Xét tam giác vuông \(IO_1O_2\):
\(O_1O_2^2=IO_1^2+IO_1^2\\ \Leftrightarrow\left(a+b\right)^2=\left(12-a\right)^2+b^2\\ \Leftrightarrow\left(a+6\right)^2=\left(12-a\right)^2+6^2\\ \Leftrightarrow12a=144-24a\\ \Leftrightarrow36a=144\\ \Rightarrow a=4\)
Tứ giác \(O_1O_2HK\) là hình bình hành, suy ra \(O_2K=O_3H=c\)
Xét tam giác vuông \(IO_3H\) ta có: \(IH^2=IO^2_3-O_3H^2=\left(12-c\right)^2-c^2\)
Xét tam giác vuông \(IKH\) :
\(KI^2=KH^2-IH^2\\ \Leftrightarrow KI^2=\left(b+c\right)^2-\left(12-c\right)^2+c^2=\left(6+c\right)^2-\left(12-c\right)^2+c^2\\ \Leftrightarrow KI^2=c^2+36c-108\\ \Rightarrow\left(O_2I-O_2K\right)^2=c^2+36c-108\\ \Leftrightarrow\left(6-c\right)^2=c^2+36c-108\\ \Leftrightarrow48c=144\Rightarrow c=3\)
Vậy \(a+b+c=4+6+3=13\left(đpcm\right)\)









