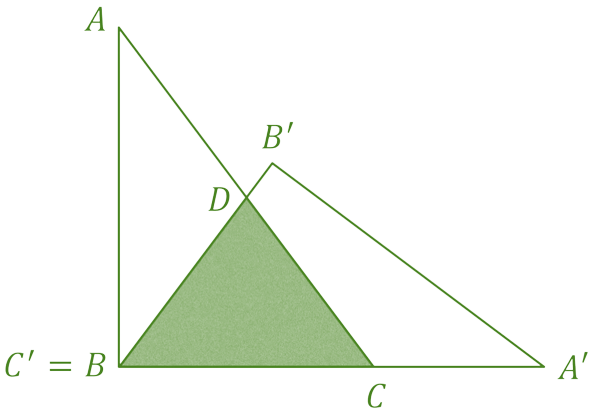
theo giả thiết thì tam giác ABC = tam giác A'B'C' và C' trùng với B nên có: góc DBC = góc DCB và góc ABB' + DBC = 90 độ
Nên góc DBA = DAB, góc
DBC = góc DCB nên tam giác ADB, BDC đều cân tại đỉnh D nên suy ra AD=BD=CD=1/2.AC
ta có: \(\dfrac{S_{DBC}}{S_{ABC}}=\dfrac{S_{DBC}}{S_{DBA'}}=\dfrac{AC}{DC}=\dfrac{1}{2}_{_{ }}\) suy ra \(\dfrac{S_{DBC}}{S_{ABC}+S_{A'B'B_{ }}}=\dfrac{S_{DBC}}{S_{DBC}+S_{BADB'A'}}=\dfrac{1}{4}\)
suy ra \(\dfrac{S_{CBD}}{S_{BADB'A'}}=\dfrac{1}{3}\)









