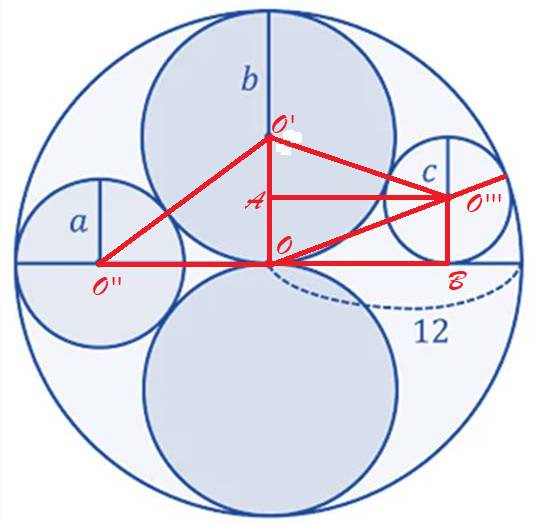
Ta có OO' = a + b
OO'' = 12 - a
Theo định lý Pytago trong tam giác OO'O'':
\(\left(a+b\right)^2=b^2+\left(12-a\right)^2\)
\(\Leftrightarrow\left(a+6\right)^2=6^2+\left(12-a\right)^2\)
\(\Leftrightarrow a^2+12a+36=6^2+144-24a+a^2\)
\(\Leftrightarrow36a=144\Rightarrow a=4\)
Lại có OO''' = 12 - c
Gọi OB là k
Áp dụng định lý Pytago trong tam giác OO'''B :
\(\left(12-c\right)^2=c^2+k^2\)
\(k^2=144-24c+c^2-c^2\Rightarrow k^2=144-24c\)
Ta có O'A = b - c
AO''' = OB = k
O'O''' = b + c
Xét tam giác AO'O''' có:
\(\left(b+c\right)^2=\left(b-c\right)^2+k^2\)
\(\Leftrightarrow b^2+2bc+c^2=b^2-2bc+c^2+144-24c\)
\(\Leftrightarrow4bc+24c=144\)
\(\Leftrightarrow24c+24c=144\)
\(\Leftrightarrow48c=144\Rightarrow c=3\)
=> a + b + c = 4 + 6 + 3 = 13









