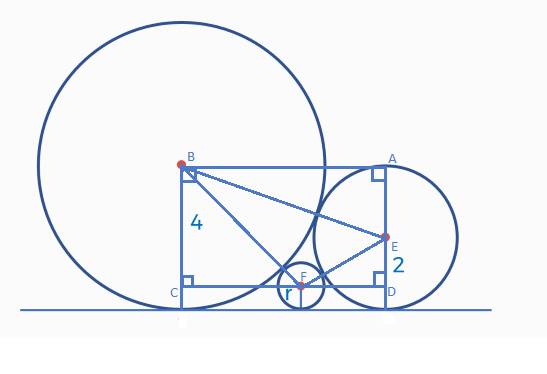
Kẻ hình như sau
Ta có BC = 4 - r
BF = 4 + r
Áp dụng định lý Pytago trong tam giác BCF ta có
\(\left(4+r\right)^2=\left(4-r\right)^2+CF^2\)
\(\Leftrightarrow16+8r+r^2=16-8r+r^2+CF^2\)
\(\Leftrightarrow CF^2=16r\)
\(\Rightarrow CF=4\sqrt{r}\)
Lại có ED = 2 - r
FE = 2 + r
Áp dụng định lý Pytago trong tam giác FED ta có
\(\left(2+r\right)^2=\left(2-r\right)^2+FD^2\)
\(\Leftrightarrow4+4r+r^2=4-4r+r^2+FD^2\)
\(\Leftrightarrow FD^2=8r\)
\(\Rightarrow FD=\left(2\sqrt{2}\right)\sqrt{r}\)
Mà \(AB=4\sqrt{r}+\left(2\sqrt{2}\right)\sqrt{r}=\sqrt{r}\left(4+2\sqrt{2}\right)\)
Ta có \(BE=4+2=6\)
Áp dụng định lý Pytago trong tam giác ABE ta có
\(36=r\left(4+2^{ }\sqrt{2}\right)^2+4\)
Giải phương trình => \(r=12-8\sqrt{2}\)









