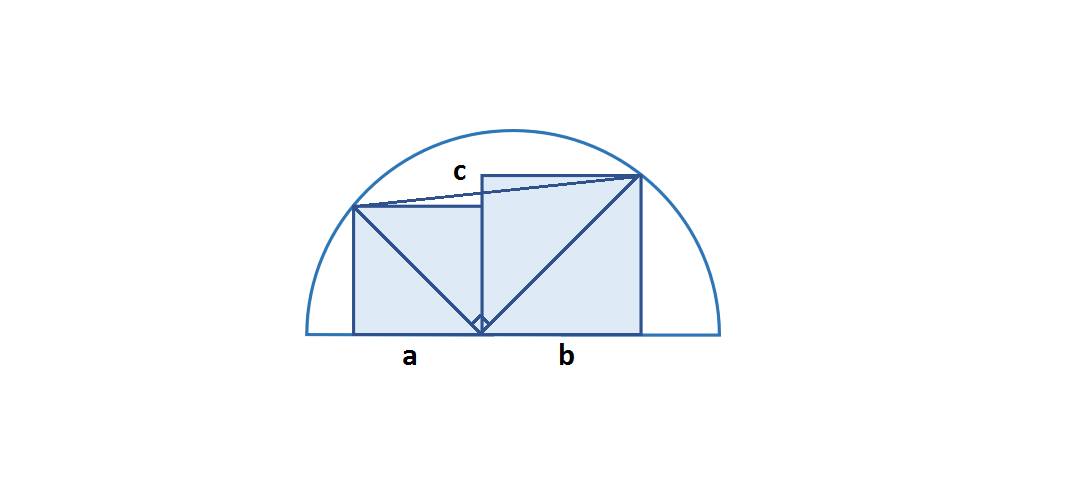
Gọi độ dài cạnh của hình vuông bên trái là a, hình vuông bên phải là b.

Vẽ 2 đường chéo của 2 hình vuông này. Ta nhận thấy góc mà hai đường chéo này tạo ra là góc vuông.

Áp dụng định lí Pytago, ta tính độ dài đường chéo của hình vuông bên trái bằng: \(\sqrt{a^2+a^2}=a\sqrt{2}\)

                                                 độ dài đường chéo của hình vuông bên trái bằng:\(\sqrt{b^2+b^2}=b\sqrt{2}\)

Lại áp dụng định lí Pytago, ta tinh được độ dài của đường thẳng có độ dài c bằng: 

     \(c^2=\left(a\sqrt{2}\right)^2+\left(b\sqrt{2}\right)^2\)

\(\Leftrightarrow c^2=2a^2+2b^2\)(*)

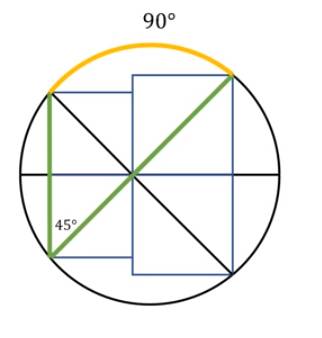
Ta sẽ tìm số đo của cung tròn màu vàng trên hình.

Sao chép một hình y hệt hình ban đầu rồi lật ngược, gắn liền với hình ban đầu tạo thành hình trên.

Ta thấy: số đo của góc nội tiếp màu xanh trên hình bằng 1 nửa góc vuông.

Áp dụng định lý góc nội tiếp ta tính được số đo của cung tròn này bằng 90^o.

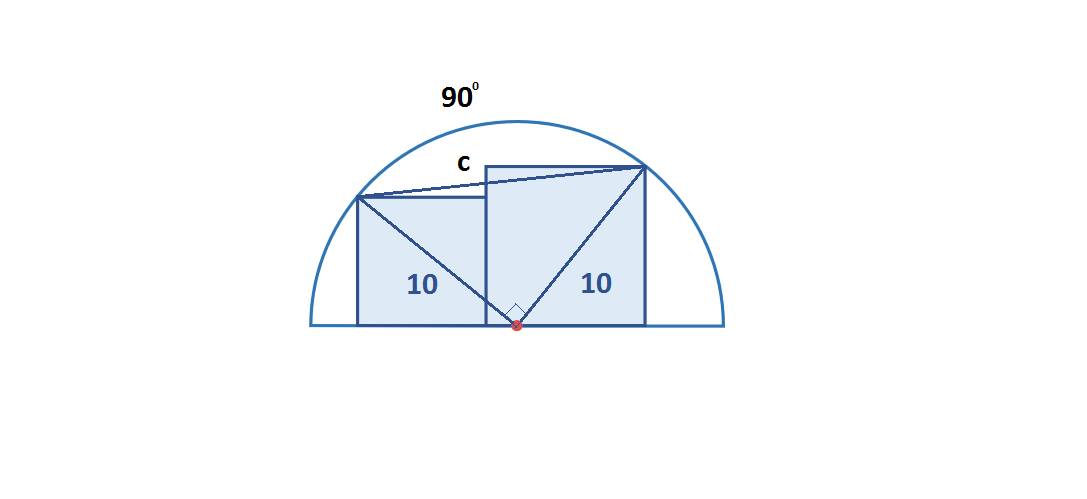
Nối 2 điểm của đoạn thẳng có độ dài c với tâm hình tròn, ta được hình trên.

Vì cung tròn trên bằng 90^o nên góc tạo từ 2 đoạn thẳng nối tâm hình tròn với 2 điểm của đoạn thẳng độ dài c cũng bằng 90^o.

Áp dụng đinh lý Pytago, ta có:

\(c^2=10^2+10^2=100+100=200\)(**)

Từ (*) và (**) ta có:

\(c^2=2a^2+2b^2=200\)

    \(=2\left(a^2+b^2\right)=200\)

    \(=a^2+b^2=200:2=100\)

Ta thấy: tổng diện tích 2 hình vuông bằng \(a^2+b^2\) mà \(a^2+b^2=100\) vậy tổng diện tích 2 hình vuông là 100 (đơn vị diện tích)