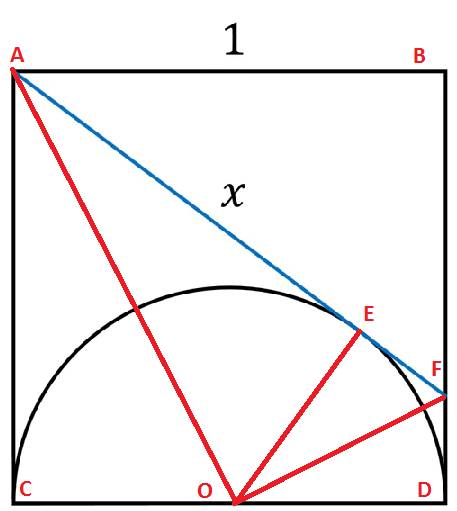
Ta thấy AB=AC=CD=DB=1 (Do ABCD là hình vuông)

⇒ CO=OE=OD (Do cùng là bán kính hình tròn tâm O)

Ta thấy AF là đường tiếp tuyến hình tròn tâm O

⇒ OE⊥AF

Xét tam giác ACO và tam giác AEO ta có: chung cạnh AO

                                                                   CO=OE 

                                                                   góc ACO= góc AEO= 90 độ

⇒ ΔACO=ΔAEO (cạnh huyền-cạnh góc vuông)

⇒ AC=AE

Chứng minh tương tự với 2 tam giác OEF và ODF

⇒ EF=FD

⇒ AF=AE+AF=AC+DF=1+DF

Có: BF=BD-FD=1-FD

Xét tam giác ABF: Theo định lí Pi-ta-go ta có:

AB²+BF²=AF²

⇒ 1+(1-DF)²=(1+DF)²

⇒ 1+1-2DF+DF²=1+2DF+DF²

⇒ 1=4DF

⇒ DF=0,25 (đơn vị)

⇒ AF=1+DF=1+0,25=1,25

⇒ x=0,25

Vậy x=0,25