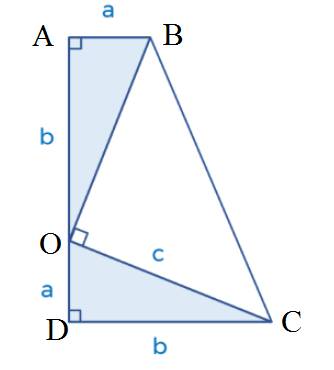
+) Ta có hình vẽ như trên.
+) Diện tích tam giác ABO vuông tại A là: \(S_{ABO}=\dfrac{ab}{2}\left(đvdt\right)\)
+) Diện tích tam giác CDO vuông tại D là: \(S_{CDO}=\dfrac{ab}{2}\left(đvdt\right)\)
+) Diện tích tam giác BOC vuông tại O là: \(S_{BOC}=\dfrac{c^2}{2}\left(đvdt\right)\)
+) Diện tích hình thang ABCD là: \(S_{ABCD}=\dfrac{\left(a+b\right)^2}{2}\)
+) Vì diện tích hình thang ABCD bằng tổng diện tích của ba tam giác ABO, CDO, và BOC nên ta có:
\(\dfrac{\left(a+b\right)^2}{2}=\dfrac{ab}{2}+\dfrac{ab}{2}+\dfrac{c^2}{2}\\ \Rightarrow\left(a+b\right)^2=2ab+c^2\\ \Rightarrow a^2+2ab+b^2=2ab+c^2\\ \Rightarrow a^2+b^2=c^2\)
Từ đấy định lí Pytago được chứng minh.









