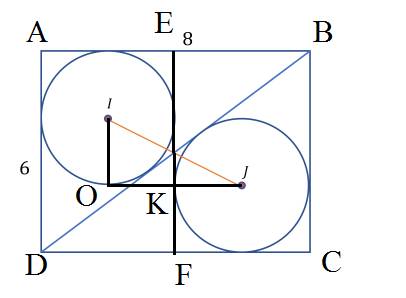
Lấy điểm O trên (I) sao cho OI // AD
Gọi trung điểm của AB và CD lần lượt là E và F
Giao điểm của EF và JO là K
Dễ dàng chứng minh được JO // AB và \(JO\perp IO\)
Ta có: \(S_{\Delta ABC}=\dfrac{AB.AD}{2}=\dfrac{6.8}{2}=24\)
\(S_{\Delta ABC}=\dfrac{\left(AB+BC+CA\right)}{2}.IO=\dfrac{\left(6+8+10\right)}{2}.IO=12.IO\)
\(\Rightarrow12IO=24\)
\(\Rightarrow IO=2\)
Tương tự như vậy ta được \(KJ=2\)
Từ đây dễ dàng chứng minh được EF vừa là tiếp tuyến của (I) vừa là tiếp tuyến của (J)
Do đó, ta tính được \(JO=2KJ=4\) và \(\Delta OJI\) vuông tại O.
Áp dụng định lý Pytago vào \(\Delta OJI\) vuông tại O ta được:
\(IJ=\sqrt{IO^2+JO^2}=\sqrt{2^2+4^2}=\sqrt{4+16}=\sqrt{20}=2\sqrt{5}\)
Vậy \(IJ=2\sqrt{5}\)









