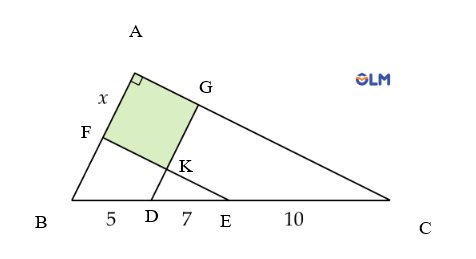
Đặt tên các điểm của tam giác như hình trên.
Áp dụng định lý Ta-lét vào tam giác EFB ta có: DK // BF ⇒ \(\dfrac{FK}{KE}=\dfrac{5}{7}\).
Khi áp dụng hệ quả của định lý Ta-lét vào tam giác ABC, ta cũng có:
\(\dfrac{FE}{AC}=\dfrac{5+7}{5+7+10}\Leftrightarrow\dfrac{FK+KE}{AC}=\dfrac{12}{22}\Leftrightarrow\dfrac{FK+\dfrac{7}{5}FK}{AC}=\dfrac{12}{22}\Leftrightarrow\dfrac{FK}{AC}=\dfrac{5}{22}\Leftrightarrow\dfrac{x}{AC}=\dfrac{5}{22}\).
Áp dụng định lý và hệ quả của định lý Ta-lét vào các tam giác tương tự ta được: \(\dfrac{x}{AB}=\dfrac{5}{11}\)
⇒ AC = 2AB. Áp dụng định lý Pi-ta-go vào tam giác ABC ta có:
\(AB^2+AC^2=BC^2\Leftrightarrow AB^2+4AB^2=\left(5+7+10\right)^2\Leftrightarrow5AB^2=22^2\Leftrightarrow AB=\dfrac{22}{\sqrt{5}}\)
\(\Rightarrow\dfrac{x}{AB}=\dfrac{5}{11}\Leftrightarrow x=\dfrac{5AB}{11}=\dfrac{5.22}{11.\sqrt{5}}=2\sqrt{5}\Rightarrow x^2=\left(2\sqrt{5}\right)^2=20\)
Vậy diện tích của phần hình tô màu là 20 (Đvdt)









