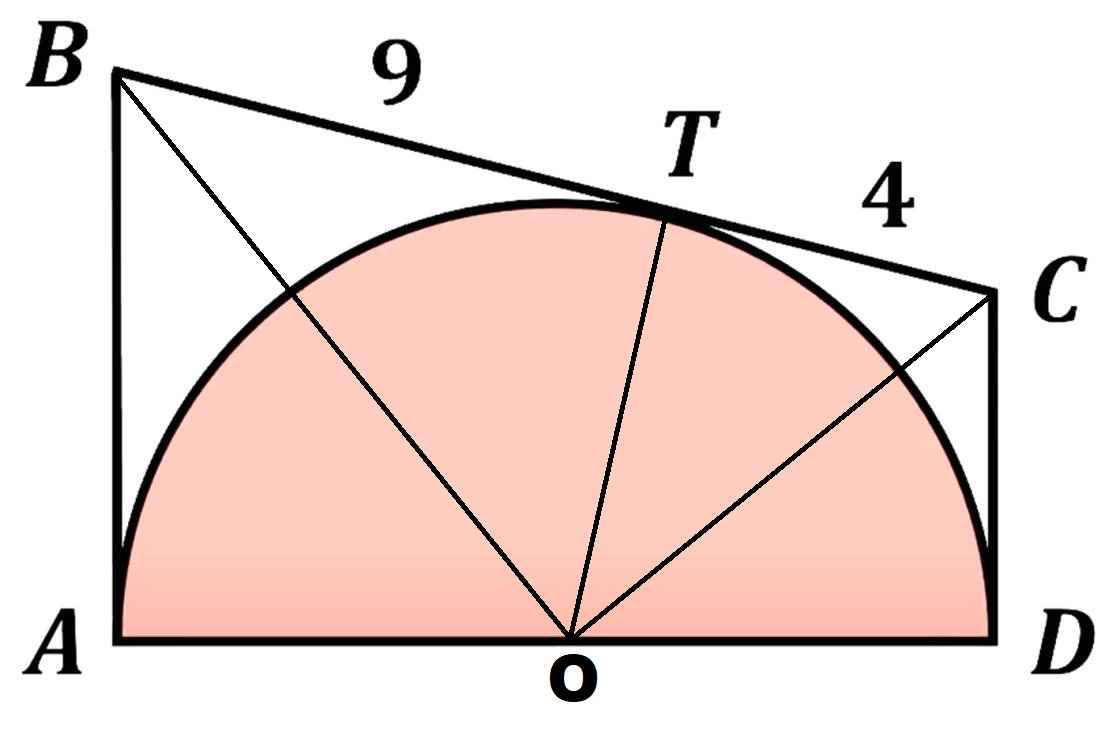
Gọi O là tâm đường tròn đường kính AD.

BA, BC, CD là tiếp tuyến của đường tròn O có tiếp điểm lần lượt là A, T, D.

Do đó BA, BC, CD vuông góc với OA, OT, OD lần lượt tại A, T, D.

Xét hai tam giác vuông ABO và TBO ta có:

\(\left\{{}\begin{matrix}OA=OT\left(bán.kính\right)\\OB=OB\end{matrix}\right.\Rightarrow\Delta ABO=\Delta TBO\left(c.c\right)\)

\(\Rightarrow\widehat{AOB}=\widehat{TOB}\) 

Suy ra OB là tia phân giác của góc AOT

Tương tự xét hai tam giác vuông DCO và TCO ta cũng có OC là tia phân giác của góc DOT

OB, OC là tia phân giác của hai góc kề bù AOT và DOT nên góc BOC = 90⁰

Xét tam giác vuông DOC ta có:

\(OT^2=TB.TC=9.4=36\)

Diện tích nửa hình tròn được tô màu bằng:

\(S=\dfrac{1}{2}.\Pi.OT^2=\dfrac{1}{2}.3,14.36=56,52\left(đvdt\right)\)

Đs....