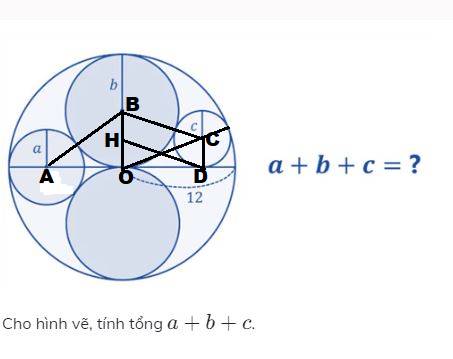
Vẽ các đoạn BO, CD vuông góc với đường kính đường tròn tâm O tại O và D.
Vẽ đường đường đi qua D song song với BC cắt BO tại H.
Dễ thấy: \(2b=12\Rightarrow b=6\)
Xét tam giác vuông \(ABO\) ta có:
\(AB^2=AO^2+OB_1^2\\ \Leftrightarrow\left(a+b\right)^2=\left(12-a\right)^2+b^2\\ \Leftrightarrow\left(a+6\right)^2=\left(12-a\right)^2+6^2\\ \Leftrightarrow12a=144-24a\\ \Leftrightarrow36a=144\\ \Rightarrow a=4\)
Tứ giác \(BCDH\) là hình bình hành, suy ra \(BH=CD=c\)
Xét tam giác vuông \(ODC\) ta có: \(OD^2=OC^2-CD^2=\left(12-c\right)^2-c^2\)
Xét tam giác vuông \(OHD\) :
\(OH^2=HD^2-OD^2\\ \Leftrightarrow OH^2=\left(b+c\right)^2-\left(12-c\right)^2+c^2=\left(6+c\right)^2-\left(12-c\right)^2+c^2\\ \Leftrightarrow OH^2=c^2+36c-108\\ \Rightarrow\left(BO-BH\right)^2=c^2+36c-108\\ \Leftrightarrow\left(6-c\right)^2=c^2+36c-108\\ \Leftrightarrow48c=144\Rightarrow c=3\)
Vậy \(a+b+c=4+6+3=13\left(đpcm\right)\)









