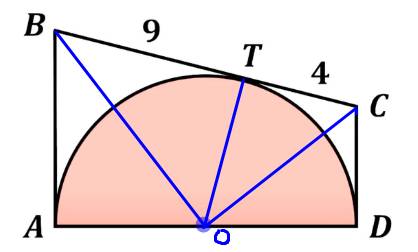
Gọi O là tâm của nửa đường tròn. Dễ thấy OB, OC lần lượt là tia phân giác của \(\widehat{AOT}\) và \(\widehat{DOT}\) . Lại có \(\widehat{AOT}+\widehat{DOT}=180^o\) nên \(OB\perp OC\) tại O. Mặt khác, BC tiếp xúc với (O) tại T nên \(OT\perp BC\) tại YT. Xét tam giác OBC vuông tại O có đường cao OT, ta có \(OT^2=TB.TC=4.9=36\Rightarrow OT=6\). Từ đó suy ra diện tích của nửa hình tròn được tô là \(\dfrac{\pi.6^2}{2}=18\pi\) (đơn vị diện tích)









