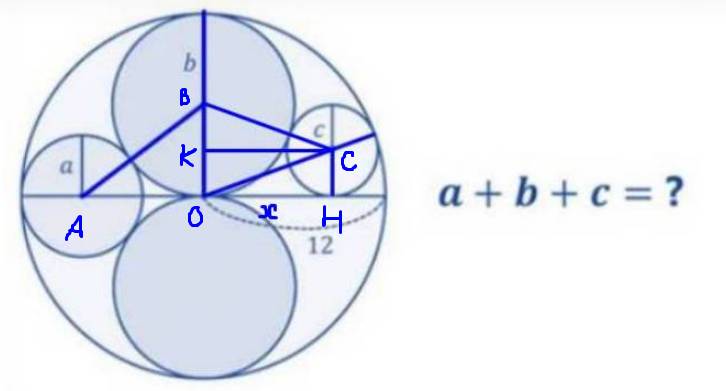
Gọi O, A, B, C lần lượt là tâm của đường tròn lớn và các đường tròn bán kính a, b, c. Hạ \(CH\perp OA\), \(CK\perp OB\). Ta thấy ngay \(2b=12\Leftrightarrow b=6\)
Mặt khác \(AB=a+6;OA=12-a\). Ta có \(AB^2=OA^2+OB^2\Leftrightarrow\left(6+a\right)^2=6^2+\left(12-a\right)^2\) \(\Leftrightarrow a^2+12a+36=36+a^2-24a+144\) \(\Leftrightarrow36a=144\Leftrightarrow a=4\)
Lại có \(BK=b-c;BC=b+c\). Đặt \(OH=CK=x\). Khi đó \(x^2=\left(b+c\right)^2-\left(b-c\right)^2=4bc=24c\)
Do \(OC=12-c\) nên từ \(OC^2=OH^2+CH^2\) nên \(\left(12-c\right)^2=x^2+c^2\) \(\Leftrightarrow c^2-24c+144=24c+c^2\) \(\Leftrightarrow48c=144\Leftrightarrow c=3\)
Từ đó suy ra \(a+b+c=13\)









